> 栈也是一种非常常见的数据结构, 并且在程序中的应用非常广泛. ### 一. 认识栈结构 > 我们先来简单认识一下栈结构, 它的特点和应用场景等. #### 栈结构 * 数组 * 我们知道数组是一种线性结构, 并且可以在数组的任意位置插入和删除数据. * 但是有时候, 我们为了实现某些功能, 必须对这种任意性加以限制. * 而栈和队列就是比较常见的受限的线性结构, 我们先来学习栈结构. * 栈（stack），它是一种运算受限的线性表,后进先出(LIFO) * LIFO(last in first out)表示就是后进入的元素, 第一个弹出栈空间. 类似于自动餐托盘, 最后放上的托盘, 往往先把拿出去使用. * 其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶，相对地，把另一端称为栈底。 * 向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素； * 从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。 * 生活中类似于栈的 * 自助餐的托盘, 最新放上去的, 最先被客人拿走使用. * 收到很多的邮件(实体的), 从上往下依次处理这些邮件. (最新到的邮件, 最先处理) * 注意: 不允许改变邮件的次序, 比如从最小开始, 或者处于最紧急的邮件, 否则就不再是栈结构了. 而是队列或者优先级队列结构. 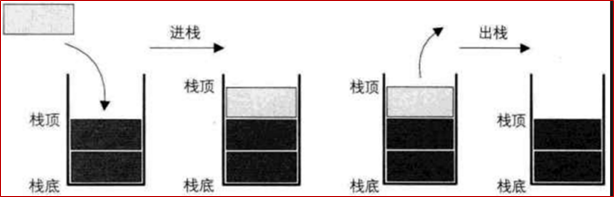* 栈结构的图解  - 程序中什么是使用栈实现的呢? - 学了这么久的编程, 是否听说过, 函数调用栈呢? - 我们知道函数之间和相互调用: A调用B, B中又调用C, C中又调用D. - 那样在执行的过程中, 会先将A压入栈, A没有执行完, 所有不会弹出栈. - 在A执行的过程中调用了B, 会将B压入到栈, 这个时候B在栈顶, A在栈底. - 如果这个时候B可以执行完, 那么B会弹出栈. 但是B有执行完吗? 没有, 它调用了C. - 所以C会压栈, 并且在栈顶. 而C调用了D, D会压入到栈顶. - 所以当前的栈顺序是: 栈顶A->B->C->D栈顶 - D执行完, 弹出栈. C/B/A依次弹出栈. - 所以我们有函数调用栈的称呼, 就来自于它们内部的实现机制. (通过栈来实现的) - 函数调用栈图解:  #### 栈面试题 * 面试题目:  * 题目答案: C * A答案: 65进栈, 5出栈, 4进栈出栈, 3进栈出栈, 6出栈, 21进栈,1出栈, 2出栈 * B答案: 654进栈, 4出栈, 5出栈, 3进栈出栈, 2进栈出栈, 1进栈出栈, 6出栈 * D答案: 65432进栈, 2出栈, 3出栈, 4出栈, 1进栈出栈, 5出栈, 6出栈 ### 二. 栈结构实现 > 我们来实现一个类, 用于模拟栈中的操作. #### 栈的创建 * 我们先来创建一个栈的类, 用于封装栈相关的操作 ```javascript // 栈类 function Stack() { // 栈中的属性 var items = [] // 栈相关的方法 } ``` * 代码解析: * 我们创建了一个Stack构造函数, 用户创建栈的类. * 在构造函数中, 定义了一个变量, 这个变量可以用于保存当前栈对象中所有的元素. * 这个变量是一个数组类型. 我们之后无论是压栈操作还是出栈操作, 都是从数组中添加和删除元素. * 栈有一些相关的操作方法, 通常无论是什么语言, 操作都是比较类似的. #### 栈的操作 * 栈常见有哪些操作呢? * `push(element)`: 添加一个新元素到栈顶位置. * `pop()`：移除栈顶的元素，同时返回被移除的元素。 * `peek()`：返回栈顶的元素，不对栈做任何修改（这个方法不会移除栈顶的元素，仅仅返回它）。 * `isEmpty()`：如果栈里没有任何元素就返回`true`，否则返回`false`。 * `clear()`：移除栈里的所有元素。 * `size()`：返回栈里的元素个数。这个方法和数组的`length`属性很类似。 * 现在我们来实现这些方法: * push方法 * 注意: 我们的实现是将最新的元素放在了数组的末尾, 那么数组末尾的元素就是我们的栈顶元素 ```javascript // 压栈操作 this.push = function (element) { items.push(element) } ``` * pop方法 * 注意: 出栈操作应该是将栈顶的元素删除, 并且返回. * 因此, 我们这里直接从数组中删除最后一个元素, 并且将该元素返回就可以了 ```javascript // 出栈操作 this.pop = function (element) { return items.pop() } ``` * peek方法 * peek方法是一个比较常见的方法, 主要目的是看一眼栈顶的元素. * 注意: 和pop不同, peek仅仅的瞥一眼栈顶的元素, 并不需要将这个元素从栈顶弹出. ```javascript // peek操作 this.peek = function () { return items[items.length - 1] } ``` * isEmpty方法 * isEmpty方法用户判断栈中是否有元素. * 实现起来非常简单, 直接判断数组中的元素个数是为0, 为0返回true, 否则返回false ```javascript // 判断栈中的元素是否为空 this.isEmpty = function () { return items.length == 0 } ``` * size方法 * size方法是获取栈中元素的个数. * 因为我们使用的是数组来作为栈的底层实现的, 所以直接获取数组的长度即可.(也可以使用链表作为栈的顶层实现) ```javascript // 获取栈中元素的个数 this.size = function () { return items.length } ``` #### 完整代码 * 下面我们给出自定义栈的完整代码: * 注意: 这里我们为了将属性方法放在一起, 没有使用原型来封装方法. ```javascript // 栈类 function Stack() { // 栈中的属性 var items = [] // 栈相关的方法 // 压栈操作 this.push = function (element) { items.push(element) } // 出栈操作 this.pop = function () { return items.pop() } // peek操作 this.peek = function () { return items[items.length - 1] } // 判断栈中的元素是否为空 this.isEmpty = function () { return items.length == 0 } // 获取栈中元素的个数 this.size = function () { return items.length } } ``` #### 栈的使用 * 我们来使用封装的栈, 模拟刚才的面试题 * 我们做了一下A, 其他大家可以自己练习一下. * C是无法使用栈来模拟的, 因为不正确的是C ```javascript // 模拟面试题 var stack = new Stack() // 情况下代码模拟 stack.push(6) stack.push(5) stack.pop() // 5 stack.push(4) stack.pop() // 4 stack.push(3) stack.pop() // 3 stack.pop() // 6 stack.push(2) stack.push(1) stack.pop() // 1 stack.pop() // 2 ``` ### 三. 栈结构应用 > 我们已经学会了如何使用`Stack`类，现在就用它解决一些计算机科学中的问题。 #### 十进制转二进制 * 为什么需要十进制转二进制? * 现实生活中，我们主要使用十进制。 * 但在计算科学中，二进制非常重要，因为计算机里的所有内容都是用二进制数字表示的（0和1）。 * 没有十进制和二进制相互转化的能力，与计算机交流就很困难。 * 如何实现十进制转二进制? * 要把十进制转化成二进制，我们可以将该十进制数字和2整除（二进制是满二进一），直到结果是0为止。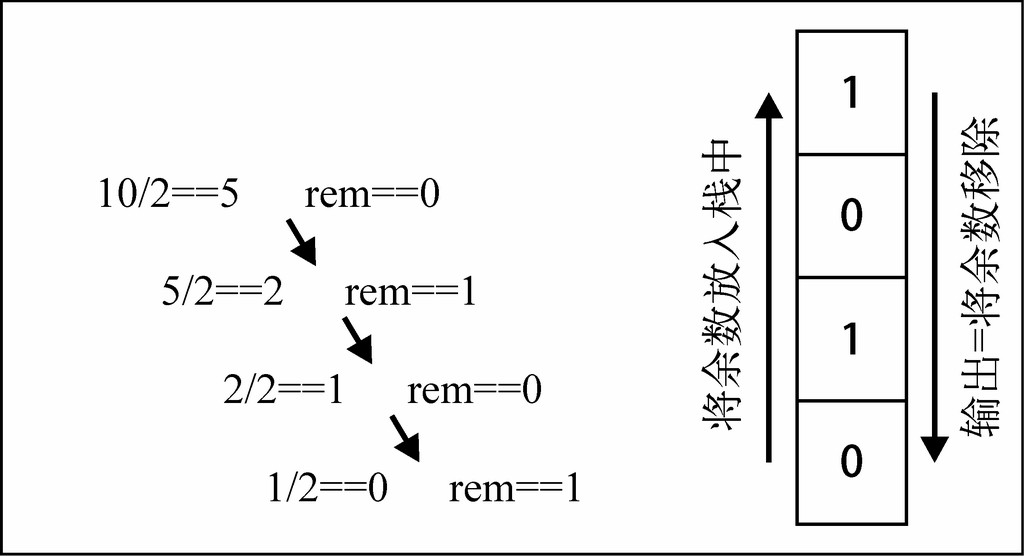 * 举个例子，把十进制的数字10转化成二进制的数字，过程大概是这样：  * 如果我们希望使用代码来实现这个功能呢? ```javascript // 封装十进制转二进制的函数 function dec2bin(decNumer) { // 定义变量 var stack = new Stack() var remainder; // 循环除法 while (decNumer > 0) { remainder = decNumer % 2 decNumer = Math.floor(decNumer / 2) stack.push(remainder) } // 将数据取出 var binayriStrng = "" while (!stack.isEmpty()) { binayriStrng += stack.pop() } return binayriStrng } ``` * 测试代码: ```javascript // 测试函数 alert(dec2bin(10)) alert(dec2bin(233)) alert(dec2bin(1000)) ``` #### 表达式运算(TODO)